Sambal / meta-irrational

Use STL lower_bound even though it’s slower

03-Jul-08

Summarizing the last few posts on STL lower_bound: instead of falling back to a naive algorithm when it’s not given a random-access iterator, STL’s lower_bound algorithm still performs binary search using bidirectional or forward-only iterators. This causes it to perform 2N list traversals, which is four times as many as the naive algorithm’s average case of N/2 list traversals. The STL algorithm guarantees that there will only be O( log N ) comparisons, but we’ve seen that’s not much of an advantage unless the comparison requires an extra memory access.

You might be thinking: why would anybody ever do lower_bound on a list anyway? Just maintain the data in a vector: that has O(1) amortized append, and the STL lower_bound wil run in O( log n ). Remember that the disadvantage of a vector is not merely the O(n) cost of inserting/deleting in the middle: adding an element to a vector invalidates all of its iterators because the addition can, in principle, realloc.

So given that, for lists, naive_lower_bound is clearer, shorter, and faster for large N even when comparisons are costly, when should you use it instead of STL lower_bound? Never. Always use STL lower_bound. The maintenance costs of naive_lower_bound are too high. If you put it in your code, even if you comment it clearly and provide a link to this discussion, in six months or two or ten years, some maintenance programmer is going to be looking at that line of code and wondering “What was wrong with STL lower_bound? Is it still true that naive_lower_bound is fast? Is it even correct?” And that maintenance programmer might well be you. It’s like the old adage: Nobody ever got fired for buying IBM. Or Microsoft. Or today, STL.

Of course, like all generalizations, this one is partially false. If your program is the client for a popular MMORPG and you offer your users a discount if they let you run numerical algorithms on their machine while the client is running, and you need to maintain a linked list of all other available clients, sorted by latency or some other simple metric of speed/quality, and frequently partition that list using lower_bound periodically, then perhaps it makes sense for you to avoid STL lower_bound. But maybe you could use a vector instead. Or maybe instead of maintaining a single sorted list, you could decide a priori to divide your clients into slow, medium, and fast links based on latency < 50ms, < 200 ms, over 200 ms. There are many available ways to approach the problem, and improving the algorithm’s running time — although it’s in some ways the easiest to measure and implement — carries with it maintenance costs that you won’t have to pay.

Filed in STL | | Comments (2) »

STL lower_bound is better for complex keys, but still loses on large N

02-Jul-08

Testing a list<int> is pretty much the worst possible case for STL’s lower bound algorithm. Recall from the analysis that STL’s lower_bound uses a binary search algorithm even when the cost of advancing an iterator N steps is O(N). The advantage of this algorithm is that it only performs O( log N ) comparisons, as opposed to O( N ) comparisons for the naive algorithm.

Testing STL lower_bound against naive_lower_bound using integers definitely plays to the strengths of naive_lower_bound: an integer compare is a single machine instruction. To test the effects of a more-costly comparison, I used the simplest costly key I could think of: a string consisting of a prefix of underscores, followed by the sequence number formatted in decimal. I ran with one, ten, and 64 underscores; 64 is the cache line length on my machine, so this length forces a comparison to make four memory accesses (two per argument) instead of only two.

For these tests, the STL lower_bound is initially twice as fast as the naive_lower_bound, and I must say it’s a bit of a relief to see the standard library algorithm outperforming the dumb algorithm. But as the cache effects start to be felt (for me, around 30,000 elements) the sheer cost of traversing the whole list twice wipes out the savings from reduced comparisons, at least for 1 and 10 underscores.

Recall from the earlier analysis that the naive algorithm runs in N * (c + t) / 2 for the average case, where c is the average cost of a comparison and t is the average cost of a list traversal. So the overall slope of the naive algorithm, for large N, should be (c + t) / 2. In contrast, the STL algorithm runs in 2 * t * N + c * lg N. Just for coarse analysis, we can throw away the c * lg N term (lg N is effectively a constant, varying between 10 and 16 when N goes from 1,000 to 60,000), which gives 2 * t for the slope of the STL algorithm. The difference between the expected slopes is (3t – c)/2.

With this in mind, you can see that even when there’s a substantial constant prefix on the key (ten underscores) this doesn’t appreciably raise the cost of a comparison, at least not compared to the cost of three list traversals. So let’s try forcing two more memory accesses per comparion by extending the prefix length to 64 bytes, the full length of a cache line.

Now the cost of a comparison is much closer to the cost of three list traversals, but still slightly less: the graph shows that the execution time of STL is still increasing more quickly with increasing N. The second memory access of the comparison doesn’t suffer the full random-access penalty of a true cache miss because the key is contiguous and the cache reads ahead, while for the list traversal it’s quite unlikely that any two adjacent list elements would be within 64 bytes of each other.

Overall, though, for most small-to-medium list sizes the STL algorithm is winning when the key is more complex than a builtin type.

Next time: why this matters, when to use the STL lower_bound, and more.

Filed in STL, Uncategorized | | Comments (0) »

STL lower_bound on lists four times slower than naive algorithm

29-Jun-08

Here is a comparison between the naive lower bound and STL’s version. Execution time reported in seconds was measured using the Windows high resolution timer. An STL list of integers 1-N was created by populating a vector, shuffling it, pushing the elements onto a list, and sorting the list. This was done so the list elements would not be allocated sequentially and thus benefit from cache locality.

For each N, 200 evenly spaced numbers in the range 1..N were selected. To these were added 0 and N+1, so that boundary conditions would be tested. The test values were shuffled to disrupt cache effects. A preliminary test was done to ensure that both algorithms got the same results for all test values. Then the lower_bound operation was timed, for each test value, repeated ten times.

As expected, the cost of memory access dominates the cost of the comparison, so the STL algorithm’s guarantee of fewer comparisons (at the cost of a guaranteed 2N memory accesses) turns out to be a bad trade. Note the knee in the graph, seen most clearly in the relative times (yellow triangles). I believe what happens there is the entire data set no longer fits in cache, and the STL algorithm suffers disproportionately from this because its first step — calculating the length of the list — causes the first elements to spill from cache as the last elements are being traversed. Then when it goes back to the beginning and starts its binary search, the first elements need to be reloaded from cache.

The results for a build with optimization turned on are similar:

In this case the Naive algorithm is consistently 4 times faster than STL, and you can clearly see the knee in the STL graph around the first tick mark — effectively there are two linear portions of the graph. Interestingly, both STL and Naive suffer similarly from cache effects, as the relative timings stay constant as we pass the knee and get to the cache-limited region. Also (though you can’t see it because I left off the values of N), the numeric value of N where the knee occurs is larger in the optimized version (45,000 vs. 20,000), probably reflecting the overhead that the debug memory allocator attaches to each block.

Filed in STL | | Comments (1) »

Visual Studio 6.0 list::sort erases some elements when more than 32767 are present

28-Jun-08

Update: This is a known bug.

In the process of gathering my data for the next post in the stl lower_bound() series, I ran into some weird timings. Basically I was seeing a linear increase until there were 32000 elements in my list, and then at 33000 the timing suddenly dropped by a factor of over 10.

I traced it back to a bug in MSVC 6.0 list::sort. I don’t know what the mechanics of the bug are, and I haven’t confirmed it widely, so I’d appreciate some feedback here. The two machines I’ve tried it on were running MSVC6.0 SP6 and had the Microsoft Platfrom SDK from February 2003 installed as well.

The repro code is below. Create a new Visual C++ Win32 console project, create an empty project, add file main.cpp, and compile. I get an assertion failure on line 34, following the second list.sort(). That is: list.sort() succeeds when there are 32767 elements in the list, but when the 32768th is added, the sort algorithm seems to be deleting 32768 elements.


#include <list>
#include <algorithm>

#include <assert.h>

using namespace std;

struct counter
{
  typedef int result_type;

  counter() : n(0) {}
  result_type operator()() { return n++; }

  result_type n;
};

int main()
{
  list<int> l;

  generate_n( back_inserter( l ), 32767, counter() );

  assert( l.size() == 32767 );
  l.sort();
  assert( l.size() == 32767 );

  l.clear();

  generate_n( back_inserter( l ), 32768, counter() );

  assert( l.size() == 32768 );
  l.sort();
  assert( l.size() == 32768 );

  l.clear();

  return 0;
}

If anyone else can reproduce this with MSVC6.0 SP6, please let me know.

Filed in Uncategorized | | Comments (2) »

Analyzing STL lower_bound: why does it iterate the whole list twice?

27-Jun-08

I criticized an STL algorithm in a previous entry, calling it “unintuitive but correct.”. That’s pretty arrogant of me, considering the STL has been published for fifteen or so years. You’d think that if an STL algorithm were incorrect, someone would have noticed by now. Or taken differently, STL doesn’t need an obscure blogger’s approval.

Anyway, we’re here to criticize algorithms here, not listen to me moan.

Here’s the naive algorithm (in C++, yet! And corrected to *cough* test the termination condition):


template< class iter, class val >
inline iter naive_lower_bound( iter l, iter u, const val& v)
{
  iter r = l;

  while( l != u && *l <= v )
  {
    r = l++;
  }

  return r;
}

Here’s the STL lower_bound algorithm from the latest version of SGI STL. (That would be v3.3 released in 2000):


template <class _ForwardIter, class _Tp, class _Distance>
_ForwardIter __lower_bound(_ForwardIter __first, _ForwardIter __last,
const _Tp& __val, _Distance*)
{
 1  _Distance __len = 0;
 2  distance(__first, __last, __len);
 3  _Distance __half;
 4  _ForwardIter __middle;
 5
 6  while (__len > 0) {
 7    __half = __len >> 1;
 8    __middle = __first;
 9    advance(__middle, __half);
10    if (*__middle < __val) {
11      __first = __middle;
12      ++__first;
13      __len = __len - __half - 1;
14    }
15    else
16      __len = __half;
17  }
18  return __first;
}

You can tell it’s an STL algorithm because it’s elegant, graceful, and full of $%! underscores. (Did Cfront need that horrible convention?)

So first let’s look at line 2. Calculating the distance() between two iterators is O(1) for a random access iterator, but O(n) for all other iterator types. The naive algorithm doesn’t calculate the distance at all.

Next think about the case where the correct lower bound is element l. The naive algorithm finds this in two list accesses: when *(l+1) is greater than v, it terminates and returns. STL walks all the way to the halfway element and inspects it first. It’s way too big, so we reduce len and partition again. We actually wind up traversing N elements to get the answer.

For the middle case or end case, a similar analysis shows that STL runs in Î©(n), about 2*N*t + C * lg N, where t and C are the average traversal and comparison costs. In contrast, the naive approach runs in an expected N*(C+t)/2 time. In the very worst case, drop the two.

So what’s the big deal? Both algorithms are O(n), differing only in a constant factor. Besides, the STL one is documented to use O(n) time but only do O(lg n) comparisons — a feature the naive algorithm notably lacks. So what’s the big deal?

The problem, in a word: caching. Next time: data!

Filed in Uncategorized | Tagged lower_bound | Comments (0) »

Unintuitive (but correct) STL lower_bound algorithm

26-Jun-08

When I was looking for a C lower-bound algorithm — after I wound up writing it myself — I realized that there was an implementation in STL.

A Detour into STL

STL, in case your programming life is lived under a rock labeled “C#”, is an awesome set of template routines for C++, for having collections, iterating over them, applying functions, and generally making C++ achieve about a tenth of the power of a language like Lisp or perl.

I’m kidding. A little.

Anyway, the cool thing about STL is that it can achieve a lot of the power of a dynamic language by using templates in clever, innovative, and (critics say) scary and evil ways. For example, not taken at random, the concept of iterators exists in STL. An iterator is a sort of generalized pointer, where (at minimum) the operations ++ and * are defined on it. If the iterator is bidirectional, then the operation — is also defined. If the iterator is random-access, then the operations +(int) and -(int) are also defined. A bare pointer is an example of a random access iterator.

So fine, we’ve built up a formalism for describing pointers and things that act like pointers but are less useful. What’s the point? The point is, through the magic of templates, you can write code that takes advantage of the features of a random-access iterator but degrades gracefully to a weaker iterator (e.g., bidirectional or forward-only), and so you can write algorithms that work on both a vector and a doubly-linked list, but give you the best available scaling for free. Not only that, this selection operates at compile-time and incurs no runtime penalty.

Sounds like magic? It is! Here’s how the advance function is implemented in STL, using python-y pseudocode:


def advance( i, n )
  case i.class of ForwardIterator
    while( n-- ) i++
  case i.class of BidirectionalIterator
    if( n >= 0 )
      while( n-- ) i++
    else
      while( n++ ) i--
  case i.class of RandomAccessIterator
    i += n

At a later date I’ll probably go into the gory details of how this selection is done in C++ at compile-time. Not because it’s not well explained at the SGI STL site and in many fine books. But because pushing the concepts out of my head into words makes them clearer in my mind. (Anyway, in brief, an ancillary type hierarchy of tag types is defined, and the compiler’s rule of selecting the most-derived matching template is exploited.)

Back to Lower Bound

For the moment let’s get back to lower bound, which is how we got here in the first place. The algorithm finds the furthest iterator in an ordered range that is still less than some test value. My naive guess as to the implementation was:


def lower_bound( l, u, v )
  case i.class of RandomAccessIterator
    # some variation of binary search
  case i.class of ForwardIterator
    lastgood = l
    while( *l < v )
      lastgood = l++
    return lastgood

So if we have a random-access capable iterator, where advancing the iterator any number of steps was O(1), we would use binary search, which gives us an overall running time of O(lg n). But if advancing the iterator n steps cost O(n), then we would use the naive linear search algorithm, for an overall average running time of O(n) and an expected cost of n/2 when the value is drawn from within the range [*l, *u).

But that’s not what the algorithm is at all. And to the strangeness (but correctness) of that, I will have to return another time, because right now I have to get to work.

Filed in Uncategorized | | Comments (4) »

Starting up a software solo practice

25-Jun-08

When I started contracting, I had just dropped out of grad school and was doing everything on a shoestring. I think we took an advance on my in-laws credit card just to buy me a machine, and my wife (who was still a grad student at that time) bought Visual Studio 6.0 Professional Edition at the Cal student store so I’d have something to hack with.

I had a copy of Wage Slave No More, which was new at that time, just published the previous year, so I learned how to set up a sole proprietorship and get a fictitious business name and business license and everything. Back in the day when some but not all of this information was available online, and you still had to (gasp) phone people.

I also read various books about business, mostly geared at middle-managers in large businesses or wannabe Donald Trump imitators. I read Rich Dad, Poor Dad. I read a lot of junk about real estate investing. I don’t think I read a lot of books aimed at small business owners or solo practitioners.

But that’s what I wound up being: not quite a real small business owner, which typically means someone with, like, inventory and premises and all that jazz. And I’m not quite a solo practitioner because our business is a partnership between me and my wife, and not just in the “You do the work, honey, and I’ll do the bookkeeping and reception” division of labor that some couples seem to adopt. We aim to be working together on each line of code that we produce and deliver to clients. We achieve that in practice I’d guess about 80% of the time, and the remaining 20% is divided between me haring off in some wild direction and occasionally bringing back some value, random open-source hackery, sysadmin work, and blogging.

So from time to time I’ll write about what it’s like to have a small software shop with no intention of growing and tell some of the stories. We’ve been up and down over the years… I think the low point was when we had agreed to buy a house, and the three months worth of client invoices that were due between the purchase agreement and the closing just kept on being due until a good two months past the closing. And then we took the money and… well, that’s best left for another time.

But accounting — or rather, bookkeeping — is where I’m going next.

Filed in Software Solo Practice | | Comments (1) »

Using precompiled headers in Visual Studio 6

24-Jun-08

I only learned how to use precompiled headers recently — even though I remember reading this paper about how to do it back in the late 90’s. It seemed like too much effort, then, and my then-blazing fast Windows NT 4.0 machine didn’t seem to need the help.

Somehow, ten years later with a dual-core CPU that’s ten times as fast, ten times as much RAM, and an effectively infinite amount of disk (1 TB on two disks), it became important enough to do. And my build times went down by a factor of three or more.

Setting up precompiled headers for the first time

Decide whether this project is going to use precompiled headers with C files or C++ files. You can’t do both, so pick the file type that there is more of.
For now let’s assume you are doing precompiled headers for C++ files.
Organize the project’s source files directory into three folders: CPP Files, C Files, and Precompiled Header. You can have subfolders under those if you want, but you must have those three folders at top level, and no C or C++ source files that are not underneath them. All C++ files that will use precompiled headers go into CPP Files. The file stdafx.cpp (the precompiled header file) goes into Precompiled Header. All other source files, typically only .c files, go into the C Files folder.
Select ‘All Configurations’.
Go to project settings, select the entire CPP Files folder, and on the C/C++ tab select “Precompiled Headers” from the Category: dropdown. Choose “Use precompiled header file (.pch)” and fill in “stdafx.h” in the “Through Header:” box.
Select the entire Precompiled Header folder, and without changing tab or category, choose “Create precompiled header file (.pch)” and fill in “stdafx.h” in the “Through Header:” box
Select the entire C Files folder, again without changing the tab or category, choose “Not using precompiled headers”
Close project settings.
Open the file stdafx.cpp and ensure that it only contains one line: #include "stdafx.h"
Open each file in the CPP files directory and ensure that the first non-comment line in that file is #include "stdafx.h". Anything before the inclusion of the precompiled header will be cheerfully ignored by the compiler. I just verified this by including a syntax error at file scope before and after the precompiled header. This failed:
```
#include "stdafx.h"
Microsoft is cool
```
while this succeeded:
```
M1cr0s0ft suxx
#include "stdafx.h"
```
Now you can proceed to move headers from the .cpp files into the precompiled header. As a rule of thumb, put all system headers (angle brackets) into the precompiled header file. Put non-system headers into the precompiled header if they are used by more than about 25% of the files in the project. Or you can obsessively time and retime rebuilds until you find the optimal distribution of headers.
Now do Build | Batch Build and choose Rebuild All. The build will appear to stall on the first C++ file, because it is precompiling the headers. Then the build of each successive file will be very quick.

Maintaining precompiled headers

When you add a new C++ file to your project, Visual Studio will helpfully select the other option from the precompiled header area — “Automatic use of precompiled headers”, also known as the evil option. As far as I can tell, this causes Visual Studio to randomly trash the precompiled header file.

This is more than merely irritating; it can introduce a circular dependency that breaks the build and makes it impossible to run your program in the debugger. If file A.cpp depends on the precompiled header in the correct way, but file B.cpp is added and depends on (and rebuilds) the precompiled header in the evil way, Visual Studio will do the following on a Rebuild All:


 compile precompiled header as per A.cpp (correctly)
 compile A.cpp
 compile precompiled header as per B.cpp (evilly and brokenly)
 compile B.cpp
 link

Then if you try to run, it notices that a dependency of A.obj is newer than A.obj, notably the .pch file. If you have incremental linking turned on, you’ll just get the “One or more files are out of date or do not exist.” dialog but the project will run.

If you later modify A.cpp and try to build to run in the debugger, then you get the message
c:\users\client\project-work\file.cpp(1) : fatal error C1852: 'DebugU/project.pch' is not a valid precompiled header file

The only cure for that is to do another Rebuild All.

There is a way to avoid this problem. It is the path of righteousness: when you add a file to a project that uses precompiled headers, you must ensure that it gets the “Use precompiled header file” option.

Deciding what to put in your precompiled header

Using precompiled headers is a sort of a devil’s bargain, really, because in order to get the speedup from using them, you wind up including the header in many more translation units. That’s not actually too painful in terms of speed, and it works great as long as you only include system headers in your precompiled header source file (stdafx.h).

Once you start including project header files, however, a change in that project file will cause the precompiled header to be invalidated, which will cause all the object files that depend on it to be invalidated, which forces you to effectively rebuild your whole project.

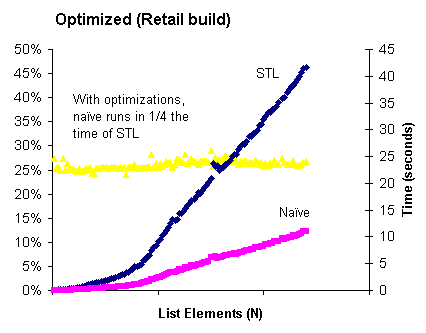
That’s fine if half your project depended on that file anyway. But it turns out not to be too painful even when it doesn’t because precompiled headers are such a big win. On one client project (40k loc, C++), a full rebuild with precompiled headers takes 20s, of which building the precompiled header is 4.5s. The full rebuild without precompiled headers takes over four minutes. Here’s a graph:

So even though we spend up to 5 seconds precompiling the header, it pays off dramatically, cutting the overall compile time by a factor of 10.

That’s not the fairest possible comparison. I haven’t spent any time tuning the header includes of the non-pch build, so I’m certainly including some headers unnecessarily into translation units that don’t need any of the things declared in those headers. I could probably spend a good half hour hunting them down, trying to make the build as tight as possible. Or I could turn on precompiled headers, get a nearly free tenfold increase in build times, and spend the half hour hacking.

Filed in Programming, Uncategorized | Tagged vs6 tips | Comments (1) »

Why I hate python

21-Jun-08

I recently wrote a small internal program in python to automate our client’s builds: run everything overnight, collect the output, and generate some rudimentary web pages It wound up being 250 loc for the program, split into about three files; and 500 loc for the tests. I spent about 2-5 days on it, part time. Just enough to give me a feel for what the language is like.

And I don’t like the language. I know that python is supposed to be the cool language, and perl is ugly line noise. And ruby? I don’t know what people have against ruby. But python is so sexy they even use it to teach the Intro to Computer Science course at Harvey Mudd now.

I hate the way formatting structures control flow. I hate that even in XEmacs in python-mode, I was fighting with it to get the right indentation (which means the right semantics). I hate that I can’t define an empty class or method. Several times I started to write a test, realized I wanted to run something first, and left it stubbed out as


  def testHTMLLine:

Well, you can’t do that. You need to do:


  def testHTMLLine:
      pass

At that point I’ll bring my own curly braces.

I hate that it’s dynamic, but not dynamic enough. I had a set of tests, collected into about five test cases. One set of tests was slow (10 seconds) because it actually tested connecting to the CVS server, checking out a project, building it, etc. The rest of the tests finished in under a second. I wanted to define a test suite that contained all the fast tests only, so I could shorten my test-code-test cycles.

Simple and evil solution: enumerate the test cases that are fast. Evil because I have to remember to update the list if I add a new fast test case. So create a suite at module level like this:


fastTests = ["test.TestParseOutputLog", "test.TestDirClass", "test.TestSystem" ]
fastSuite = unittest.TestLoader().loadTestsFromNames( fastTests )

Clever and dynamic solution: enumerate all the tests but remove the slow ones.

# NOTE: not actually python, this DOESN'T WORK
fastTests = __thismodule__.Classes.remove( "SlowTest" )
fastSuite = unittest.TestLoader().loadTestsFromNames( fastTests )

I couldn’t figure out how to easily enumerate all the classes in the module I was in. While loading the module, some of the things which get set up eventually (the module object, for example) are not yet available to me. Look, I know it’s possible because the unittest.main() routine knows how to enumerate all the classes which are descended from unittest.TestCase. But it’s not trivial to do. In ruby you could do something like

fastTests = []
ObjectSpace.each_object( Class ) { |x| fastTests << x.to_s if x =~ /^Test/ }
fastTests.delete("TestSlow")

where you could filter on name (starts with Test) and file (if necessary), and then remove the slow one. This isn’t about dynamic vs. static languages, it’s about user experience. In C you know you can’t do reflection, and when a unit test framework like cxxtest depends on perl or Python being installed, that’s fine. But because it’s possible in Python — but obscure and ill-documented — it becomes an annoyance.

The documentation is horrible. Over the last ten years my first recourse when looking for API documentation has been my friend Google. The Python documentation, even though it’s all free and available online, seems to be deliberately poorly organized and indexed. What I was hoping for was a quick cheat sheet on how to do a common thing (string interpolation). What I found was proposals to change or extend Python in varying mutually incompatible ways, in order to make it easier to do string interpolation. And this experience was repeated over and over as I dug through the language, library, and ancillary documentation looking for the Python way to do the things I needed.

Finally, Python doesn’t live up to its hype. How can it support functional programming when expression if (as opposed to statement if) was only added as a language feature in version 2.5? Even C has it!

Perhaps I have this all wrong, and Python is the best language EVAH. In the spirit of Strong Opinions, Weakly Held I welcome corrections and arguments in the comments.

Filed in Languages | Tagged python sucks | Comments (16) »

When backslashes attack (or: rsync sucks)

20-Jun-08

We use BackupPC for our backups, both on our site and at $CLIENT. It’s a great onsite backup tool, really brilliantly done, and I recommend it to anyone who has small office multi-PC backup needs.

BackupPC can connect to clients in a variety of ways, the most useful being rsync and SMB (windows networking). All our machines are on rsync and most of $CLIENT’s are on SMB, just because it was easier to use the networking that was already set up than to install rsync on 20 machines.

Recently we switched a key computer to rsync because it had been having problems with SMB. I got most of the files being backed up but there was a problem with the Documents and Settings directory, which is, um, important. So I hacked on the config files for a while and couldn’t get it to work. I eventually split all but the Documents and Settings directory into its own host so at least that stuff (accounting databases) would be being backed up.

It turns out that the problem was one character in the host’s rsyncd.conf file. This may be fixed with new versions of rsync, but just for your information you will get a ‘chdir error’ if there’s a trailing backslash in your path, like this:

[docs]
path = C:\Documents and Settings\

but everything works fine if the backslash is gone, like this:

[docs]
path = C:\Documents and Settings

Filed in BackupPC | Tagged BackupPC, rsync, Sysadmin | Comments (0) »

Recent Posts