Sambal

Testing a list<int> is pretty much the worst possible case for STL’s lower bound algorithm. Recall from the analysis that STL’s lower_bound uses a binary search algorithm even when the cost of advancing an iterator N steps is O(N). The advantage of this algorithm is that it only performs O( log N ) comparisons, as opposed to O( N ) comparisons for the naive algorithm.

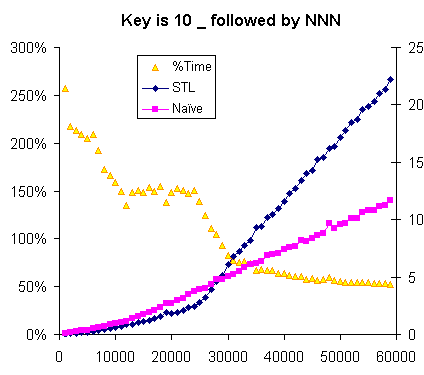
Testing STL lower_bound against naive_lower_bound using integers definitely plays to the strengths of naive_lower_bound: an integer compare is a single machine instruction. To test the effects of a more-costly comparison, I used the simplest costly key I could think of: a string consisting of a prefix of underscores, followed by the sequence number formatted in decimal. I ran with one, ten, and 64 underscores; 64 is the cache line length on my machine, so this length forces a comparison to make four memory accesses (two per argument) instead of only two.

For these tests, the STL lower_bound is initially twice as fast as the naive_lower_bound, and I must say it’s a bit of a relief to see the standard library algorithm outperforming the dumb algorithm. But as the cache effects start to be felt (for me, around 30,000 elements) the sheer cost of traversing the whole list twice wipes out the savings from reduced comparisons, at least for 1 and 10 underscores.

Recall from the earlier analysis that the naive algorithm runs in N * (c + t) / 2 for the average case, where c is the average cost of a comparison and t is the average cost of a list traversal. So the overall slope of the naive algorithm, for large N, should be (c + t) / 2. In contrast, the STL algorithm runs in 2 * t * N + c * lg N. Just for coarse analysis, we can throw away the c * lg N term (lg N is effectively a constant, varying between 10 and 16 when N goes from 1,000 to 60,000), which gives 2 * t for the slope of the STL algorithm. The difference between the expected slopes is (3t – c)/2.

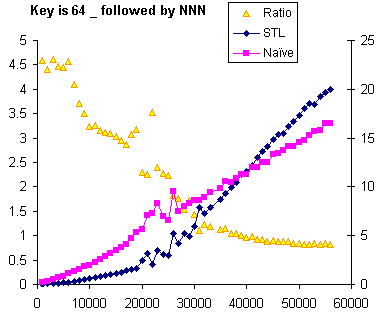
With this in mind, you can see that even when there’s a substantial constant prefix on the key (ten underscores) this doesn’t appreciably raise the cost of a comparison, at least not compared to the cost of three list traversals. So let’s try forcing two more memory accesses per comparion by extending the prefix length to 64 bytes, the full length of a cache line.

Now the cost of a comparison is much closer to the cost of three list traversals, but still slightly less: the graph shows that the execution time of STL is still increasing more quickly with increasing N. The second memory access of the comparison doesn’t suffer the full random-access penalty of a true cache miss because the key is contiguous and the cache reads ahead, while for the list traversal it’s quite unlikely that any two adjacent list elements would be within 64 bytes of each other.

Overall, though, for most small-to-medium list sizes the STL algorithm is winning when the key is more complex than a builtin type.

Next time: why this matters, when to use the STL lower_bound, and more.